Batch Update: LBG

• Common Properties and Notational Conventions
• Java implementation
  

The LBG (or generalized Lloyd) algorithm (Forgy, 1965; Linde et al., 1980; Lloyd, 1957) works by repeatedly moving all reference vectors to the arithmetic mean of their Voronoi sets. The theoretical foundation for this is that it can be shown (Gray, 1992) that a necessary condition for a set of reference vectors to minimize the distortion error

is that each reference vector fulfills the centroid condition. In the case of a finite set of input signals and the use of the Euclidean distance measure the centroid condition reduces to
 
whereby is the Voronoi set of unit c.

The complete LBG algorithm is the following:

1.

Initialize the set to contain N () units

with reference vectors chosen randomly (but mutually different) from the finite data set .

2.

Compute for each unit its Voronoi set .

3.

Move the reference vector of each unit to the mean of its Voronoi set:

4.

If in step 3 any of the did change, continue with step 2.

5.

Return the current set of reference vectors.

The steps 2 and 3 together form a so-called Lloyd iteration, which is guaranteed to decrease the distortion error or leave it at least unchanged. LBG is guaranteed to converge in a finite number of Lloyd iterations to a local minimum of the distortion error function (see figure 4.1 for an example).

 
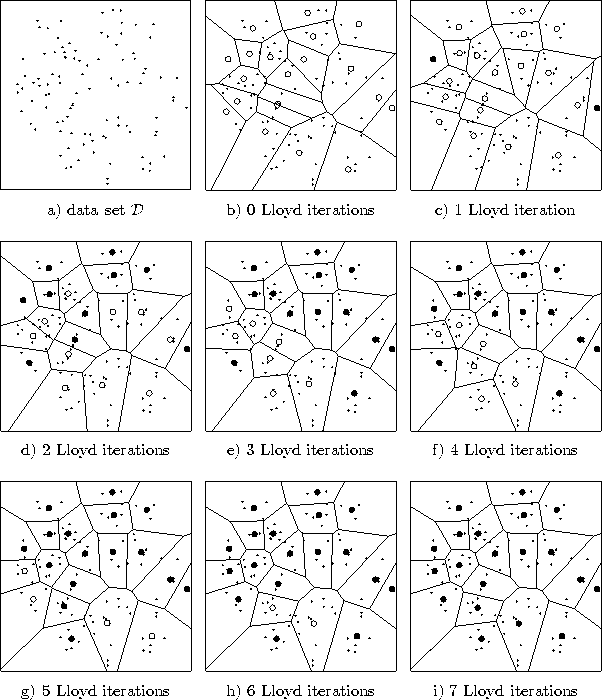
Figure 4.1:  LBG simulation. a) The data set consisting of 100 data items. b) 20 reference vectors have been initialized randomly from points in . The corresponding Voronoi tessellation is shown. c-i) The positions of the reference vectors after the indicated number of Lloyd iterations. Reference vectors which did not move during the previous Lloyd iteration are shown in black. In this simulation LBG has converged after 7 Lloyd iterations.

An extension of LBG, called LBG-U (Fritzke, 1997), is often able to improve on the local minima found by LBG. LBG-U performs non-local moves of single reference vectors which do not contribute much to error reduction (and are, therefore, not useful, thus the ``U'' in LBG-U) to locations where large quantization error does occur. Thereafter, normal LBG is used to find the nearest local minimum of the distortion error function. This is iterated as long as the LBG-generated local minima improve. LBG-U requires a finite data set, too, and is guaranteed to converge in a finite number of steps.