k-means

• Common Properties and Notational Conventions
• Java implementation not (yet) available

Instead of having a constant learning rate, we can also decrease it over time. A particularly interesting way of doing so is to have a separate learning rate for each unit and to set it according to the harmonic series:

Thereby, the time parameter t stands for the number of input signals for which this particular unit has been winner so far. This algorithm is known as k-means (MacQueen, 1967), which is a rather appropriate name, because each reference vector is always the exact arithmetic mean of the input signals it has been winner for so far. The sequence of successive values of is the following:

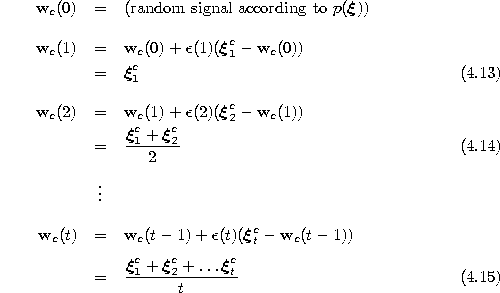
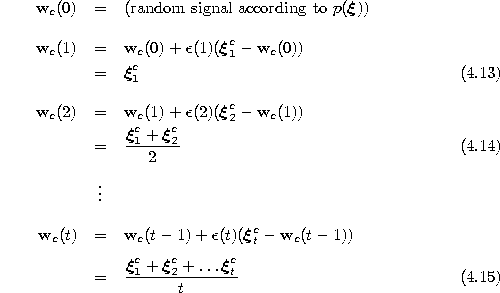
One should note that the set of signals for which a particular unit c has been winner may contain elements which lie outside the current Voronoi region of c. The reason is that each adaptation of changes the borders of the Voronoi region . Therefore, although represents the arithmetic mean of the signals it has been winner for, at time t some of these signal may well lie in Voronoi regions belonging to other units.

Another important point about k-means is, that there is no strict convergence (as is present e.g. in LBG), the reason being that the sum of the harmonic series diverges:

Because of this divergence, even after a large number of input signals and correspondingly low values of the learning rate arbitrarily large modifications of each input vector may occur in principal. Such large modification, however, are very improbable and in simulations where the signal distribution is stationary the reference vectors usually rather quickly take on values which are not much changed in the following. In fact, it has been shown that k-means does converge asymptotically to a configuration where each reference vector is positioned such that it coincides with the expectation value
 
of its Voronoi region (MacQueen, 1965). One can note that (4.17) is the continuous variant of the centroid condition (4.2). Figure 4.5 shows some stages of a simulation for a simple ring-shaped data distribution. Figure 4.6 displays the final results after 40000 adaptation steps for three other distribution.

 
Figure 4.5:   k-means simulation sequence for a ring-shaped uniform probability distribution. a) Initial state. b-f) Intermediate states. g) Final state. h) Voronoi tessellation corresponding to the final state. The final distribtion of the reference vectors still reflects the clusters present in the initial state (see in particular the region of higher vector density at the lower left).

 
Figure:   k-means simulation results after 40000 input signals for three different probability distributions (described in the caption of figure 4.4).